离散数学是逻辑的基石，而集合论则是这块基石的灵魂。

---

前言

在深耕 OpenHarmony 跨平台开发的旅途中，我们往往会被繁琐的业务逻辑所包围。特别是当面对“多维联动筛选”、“权限逻辑判定”等场景时，代码中极易出现层层嵌套的 if-else。这不仅降低了代码的可读性，更埋下了难以排查的 Bug 隐患。

本文作为本系列的开篇，旨在引导读者回归逻辑的本质——集合论。我们将探讨如何利用集合的交、并、补运算，将复杂的 UI 状态转换抽象为纯粹的数学推导。在 Flutter 简洁的声明式语法下，集合论将赋予应用前所未有的健壮性与表现力。

---

目录

1. 集合论的基本概念与 UI 映射
2. 业务逻辑的数学建模
3. 系统架构设计 (UML & 流程)
4. Flutter 核心代码实现
5. 实战案例演练
6. 总结与展望

---

一、 集合论的基本概念与 UI 映射

在计算机科学中，集合（Set）是由一组无序且唯一的元素组成的整体。在 Flutter 开发中，我们可以将每一个 UI 状态 或 业务数据实体 视为集合中的一个元素。

1. 核心运算定义

集合运算	数学符号	逻辑语义	Flutter 对应方法	业务典型案例
并集 (Union)	$A\cup B$	逻辑“或” (OR)	setA.union(setB)	多角色权限合并
交集 (Intersection)	$A\cap B$	逻辑“与” (AND)	setA.intersection(setB)	多重条件联合筛选
补集/差集 (Difference)	$A-B$	逻辑“非” (NOT)	setA.difference(setB)	黑名单/排除已选

---

二、 业务逻辑的数学建模

假设我们在开发一个适配鸿蒙系统的商城应用，其核心需求是实现一个高性能的商品过滤系统。

1. 定义全集 $U$：当前商场中上架的所有商品集合。

2. 定义属性子集：

   • $C_{phone}$：分类为“手机”的商品集合。
   • $C_{pc}$：分类为“平板”的商品集合。
   • $P_{budget}$：价格在 $0\sim 2000$ 之间的商品集合。
   • $S_{instock}$：当前有库存的商品集合。

3. 构建逻辑方程：
   若用户想看“手机或平板”，且价格在预算内、必须有货，则结果集 $R$ 为：
   [ R = (C_{phone} \cup C_{pc}) \cap P_{budget} \cap S_{instock} ]

---

三、 系统架构设计

为了清晰地展现集合逻辑在代码中的流转，我们引入 UML 类图与业务流程图。

1. 业务流程图 (Flowchart)

2. 系统类图 (UML)

---

四、 Flutter 核心代码实现

在 Dart 中，Set 对象的底层实现对集合运算进行了高度优化。相比于 List.where 的线性查找，合理利用 Set 的哈希特性可以显著提升大规模数据下的过滤性能。

核心代码片段：

// 1. 分类匹配：通过并集操作合并多个选中的分类
Set<Product> getCategorySet() {
  if (selected.isEmpty) return allProducts;
  return allProducts.where((p) => selected.contains(p.category)).toSet();
}

// 2. 最终筛选：应用交集公式
void updateResults() {
  var categorySet = getCategorySet();
  var priceSet = allProducts.where((p) => p.price <= limit).toSet();
  
  // R = C ∩ P
  var result = categorySet.intersection(priceSet);
}

---

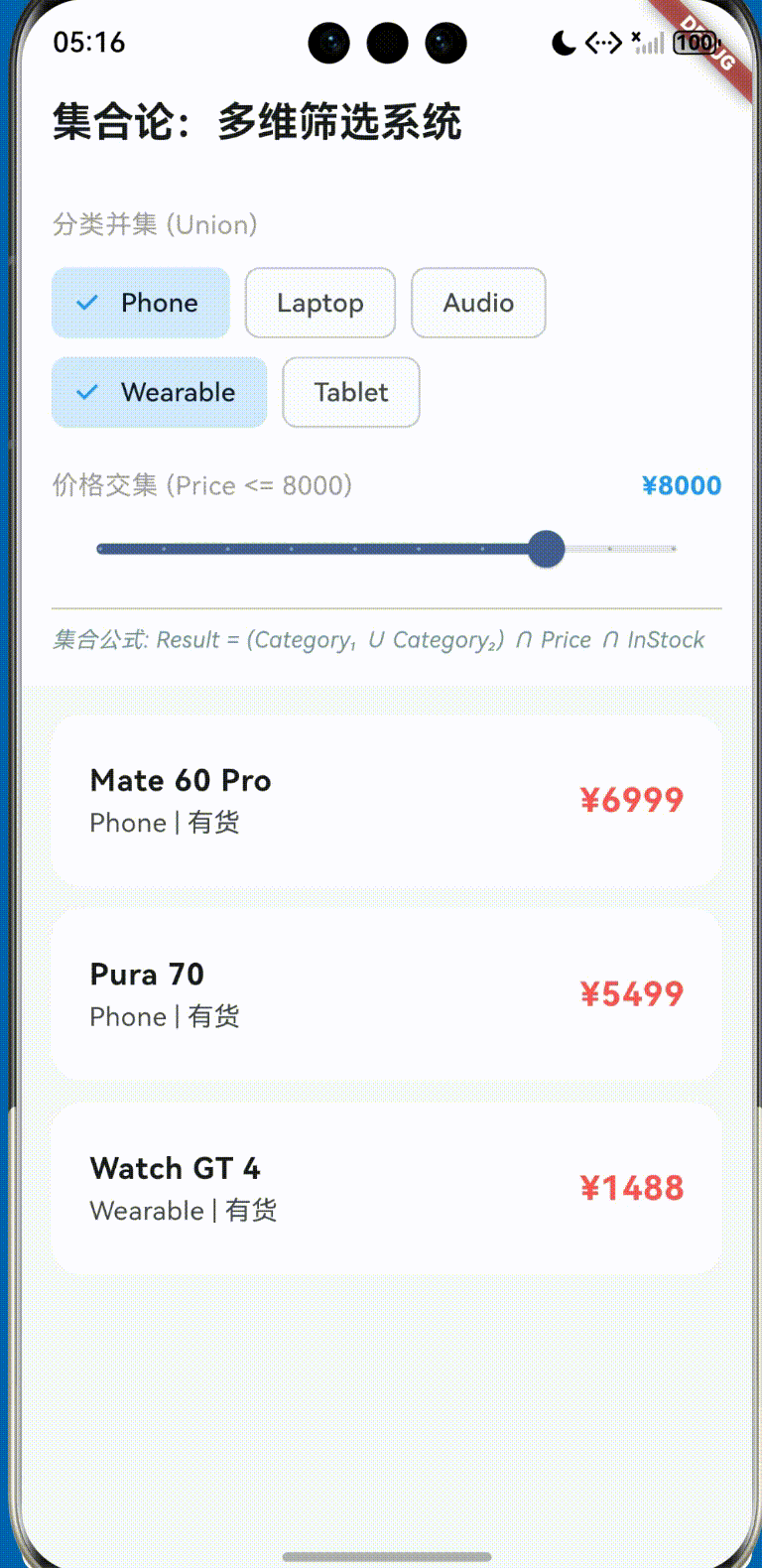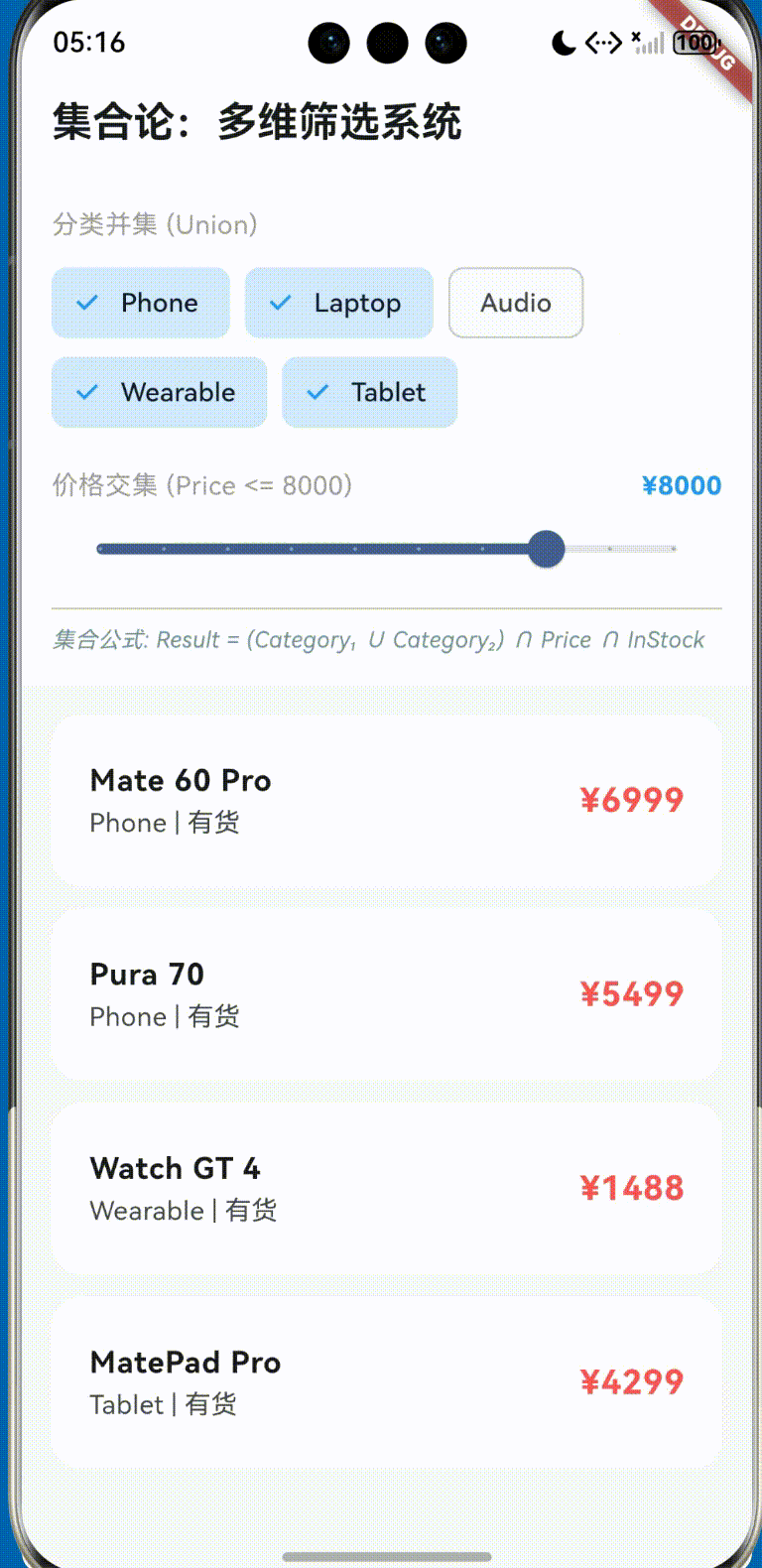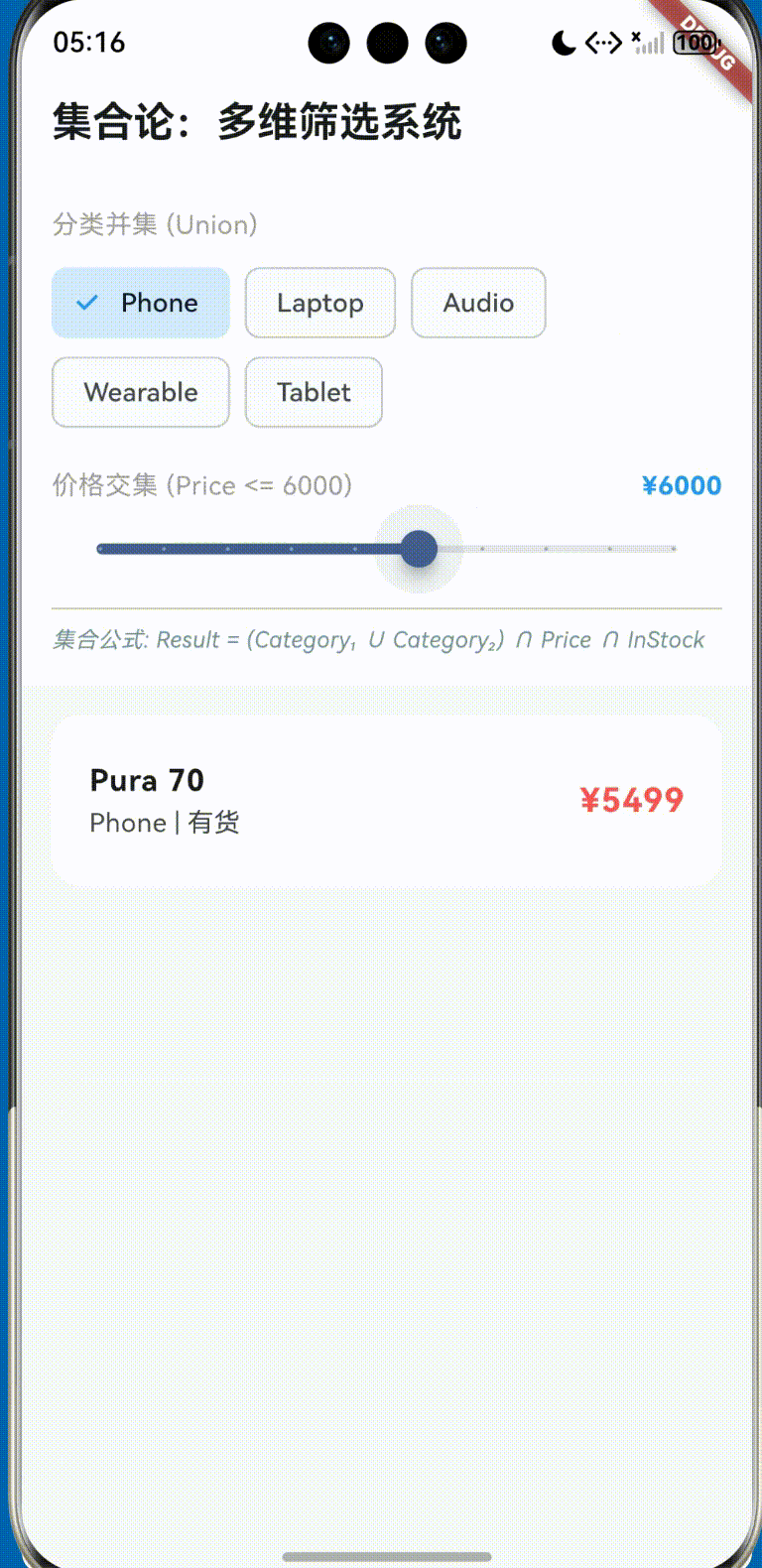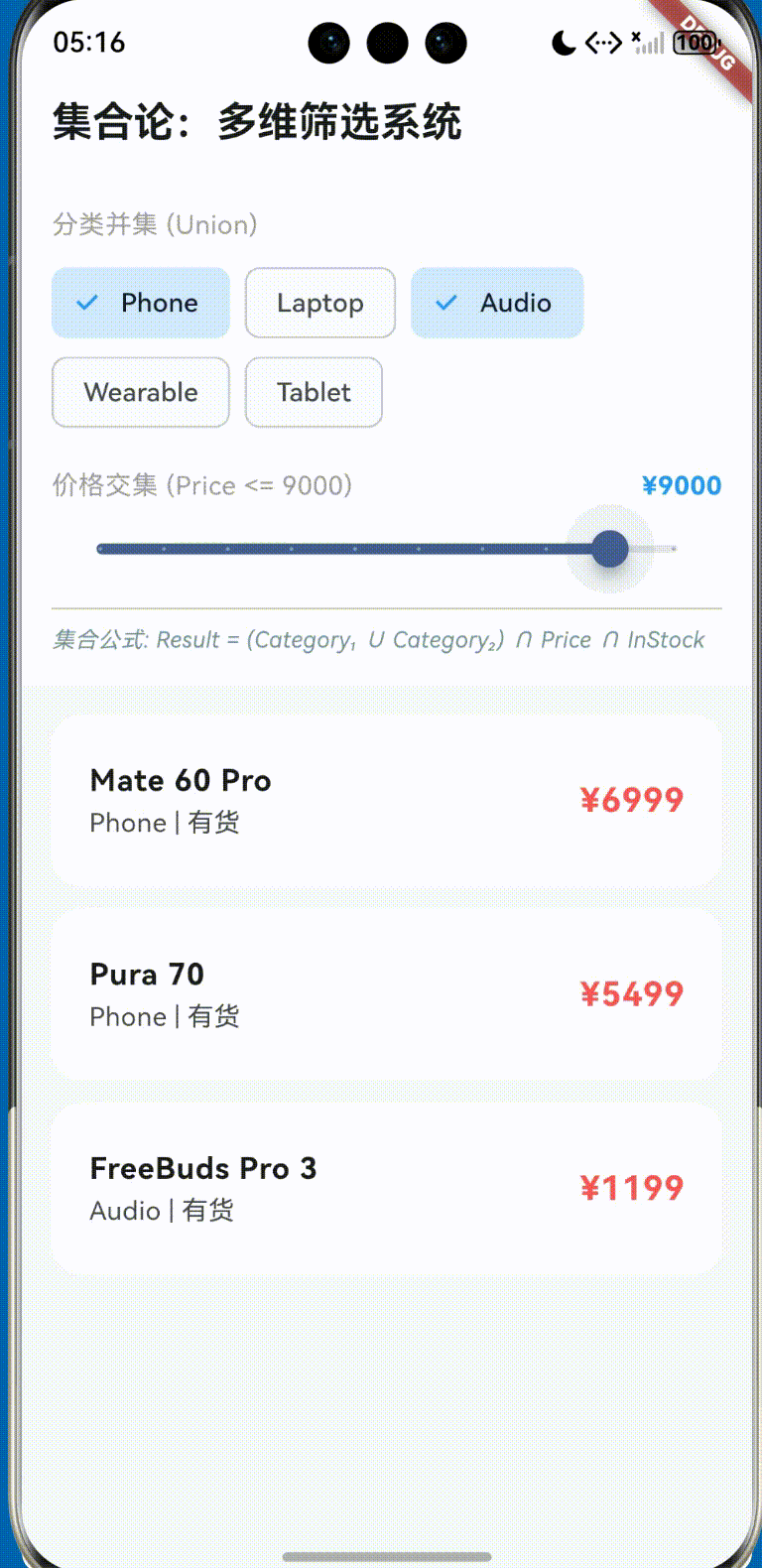
五、 实战案例演练

我们将以上理论付诸实践，构建一个名为 “Harmony Discrete Filter” 的应用。其代码逻辑完全遵循上述数学模型。

(详细代码已在项目 lib/main.dart 中实现，具备完整的响应式交互体验)

---

六、 总结与展望

通过集合论，我们成功地将复杂的业务判断抽象为纯粹的数学运算。在鸿蒙跨平台开发中，这种“逻辑前置”的思维方式能带来以下收益：

• 逻辑确定性：数学公式不会因为页面生命周期的变化而产生歧义。
• 极致性能：利用哈希集合的特性，将复杂度控制在 $O(n)$ 以内。
• 解耦设计：UI 只负责渲染集合结果，而不必关心过滤逻辑的细节。

下一篇预告：我们将深入探讨命题逻辑，解析布尔代数如何驱动 Flutter 的响应式引擎，敬请期待。

---

欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net